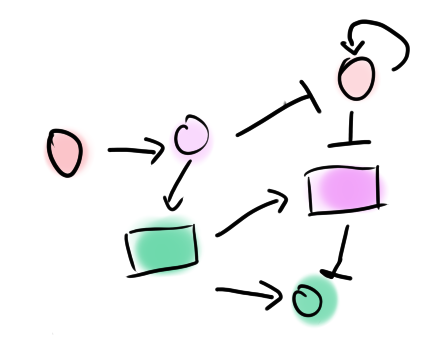
Many things in nature are periodic in time - they repeat on a regular basis. The Earth goes around the sun every year and turns around its axis every day. Such repeating phenomena are also present in biology. We have our internal 24-hour rhythm, which is aligned with day and night cycles: the circadian clock. Other examples are the cell division cycle or the segmentation clock, which is important in the development of vertebrates. This oscillatory behavior is typically generated by a complex network of interacting genes and proteins, and what is oscillating is typically the concentration or activity of the proteins involved. Mathematical modeling of these interaction networks can show us which mechanisms can lead to oscillations and in which parameter regimes we can find them.

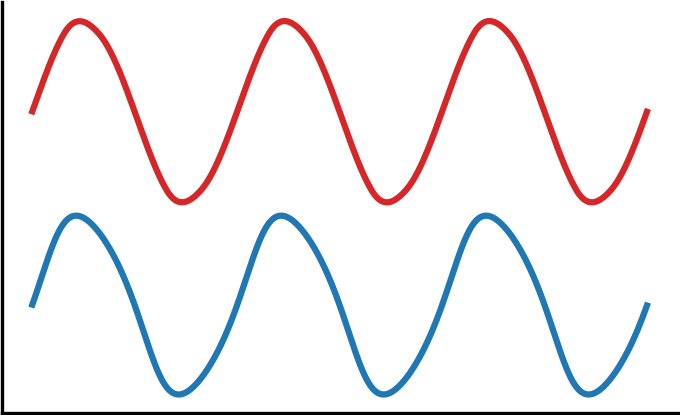
When different oscillators are coupled, they may influence each others' progress through their cycle and synchronize. Understanding the conditions necessary for this synchronization is important for many different applications, and again, mathematical modeling has been instrumental for the investigation of such systems.

Stripes on zebras, spots of vegetation, the formation of fingers on our hands, ... These are all examples of biological systems that exhibit regular patterns. The mathematical study of pattern formation goes back to the work of Alan Turing, who besides his groundbreaking work on the first computers also proposed a mathematical model for `morphogenesis' --- the establishment of form. In developmental systems, pattern formation is important to generate functional structures.

I am interested in mathematical models of pattern formation, mainly in the context of collections of cells. Both chemical signaling and mechanical aspects, such as cell density and motility, can lead to pattern formation. Moreover, patterns are modified depending on the shape and size of the domain on which they form. I am interested in understanding such patterning mechanisms in biological systems and analyzing patterns from experimental data.

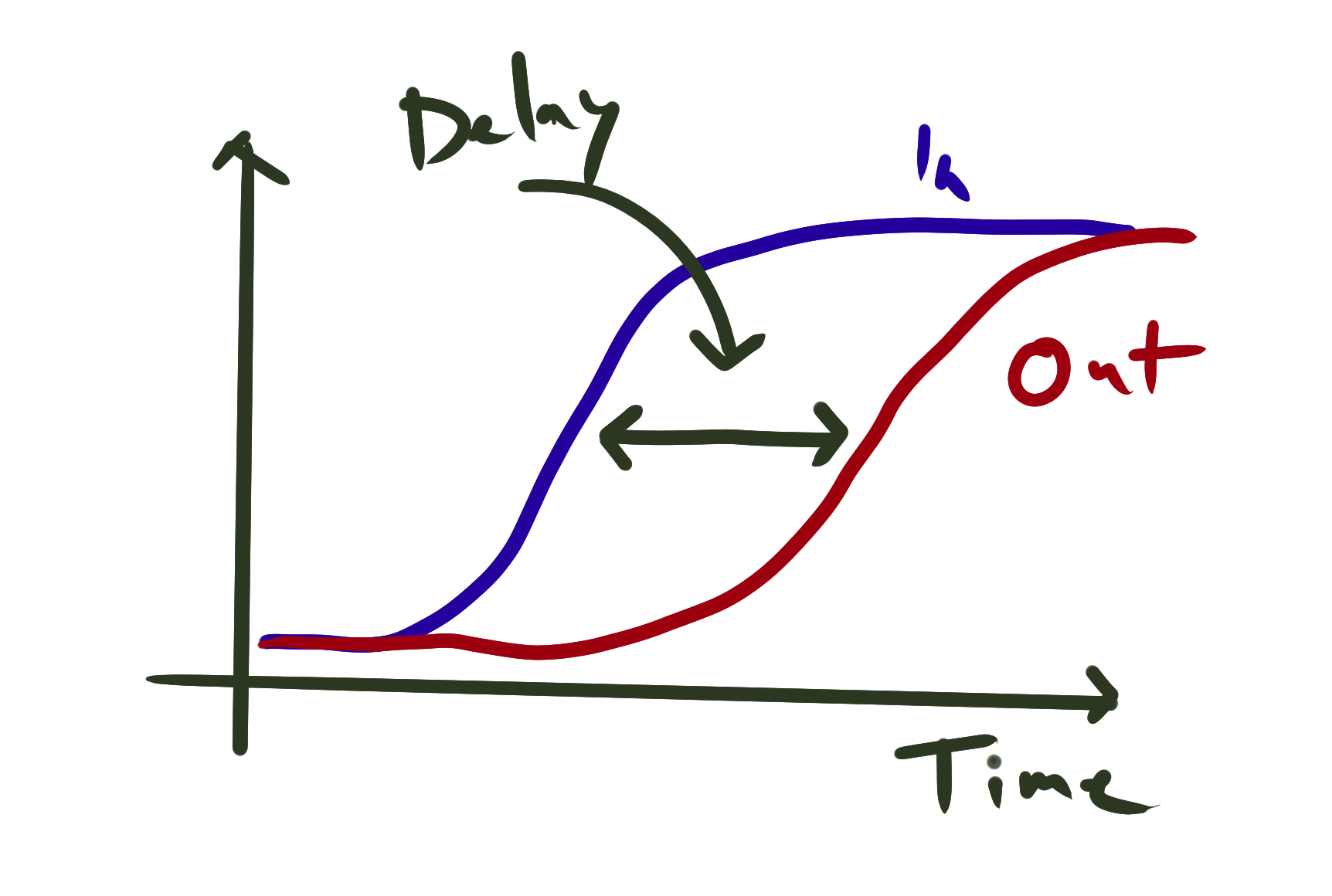
Many systems include some kind of memory, or time lags. You can think of the time for a signal to travel from one place to another, for example. In biological systems, such time delays are also present. The time it takes for a whole chain of reactions to happen, or for molecules to be transported from one location in the cell to another, may cause such a delay. The fact that interactions are not immediate can play an important role in the dynamics. Combined with negative feedback, time delays often lead to oscillations, but they can have other interesting effects.

Mathematically, you can use delay differential equations to model these systems. Here, the time delay is explicitly introduced into the mathematical equations describing the system. The benefit of using such an equation is that many, possibly unknown, mechanisms can be summarized into a single parameter: the time delay.

I am interested in using analytical and numerical methods to examine the behavior of such delayed systems, with a focus --- again --- on oscillatory systems. I have also worked on systems with a time delay that are coupled in space through diffusion, in which case pattern formation and traveling waves can appear.

Since my studies in Complex Systems Science, I retain an interested in this very broad field. During my Master's I worked on projects related to epidemiology and climate dynamics. The climate model I studied also shows oscillations, with mechanisms not unlike those I now look at in biological systems.

In 2019 I attended the winter workshop in complex systems, and collaborated on a project in which we set up a model of a railway network. We derived a diffusion-like equation to describe how train delays can dissipate through the whole network. The collaboration resulted in this paper.